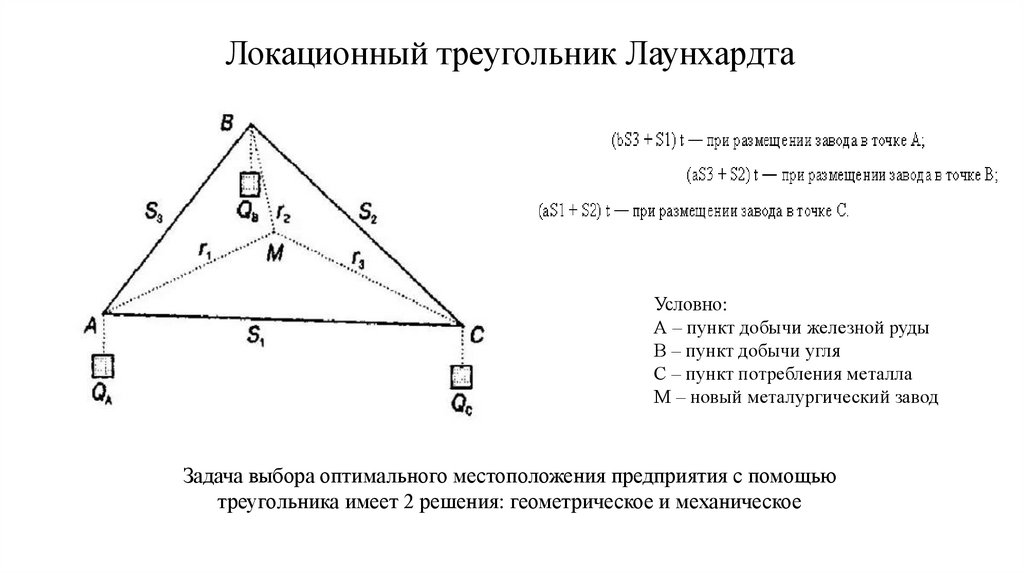
Треугольник Лаунхардта – одна из захватывающих геометрических фигур, обладающая множеством свойств и применений в математике и физике. Имя этого треугольника происходит от немецкого математика Карла Лаунхардта, который впервые исследовал особенности этой фигуры в 1833 году.
Треугольник Лаунхардта имеет интересную геометрическую структуру, состоящую из трех равных прямоугольных треугольников, размещенных внутри крупного равностороннего треугольника. Две из этих прямоугольных треугольников являются зеркальными отражениями друг друга относительно гипотенузы крупного треугольника.
Основное свойство треугольника Лаунхардта заключается в том, что сумма площадей трех прямоугольных треугольников внутри него равна площади самого крупного треугольника. Это может быть представлено следующей формулой: S = a²/2, где a – длина стороны крупного треугольника.
Треугольник Лаунхардта находит свое применение в различных областях науки и техники. Например, его особенности используются в строительстве и архитектуре для создания прочных и устойчивых конструкций. Благодаря своим уникальным свойствам, треугольник Лаунхардта привлекает внимание исследователей и ученых со всего мира, которые продолжают расширять области его применения и изучать его особенности.
Треугольник Лаунхардта: определение, свойства и применение
Треугольник Лаунхардта обладает следующими свойствами:
- Угол, образованный биссектрисами треугольника Лаунхардта, равен 120 градусов.
- Биссектрисы каждого угла треугольника Лаунхардта делят противоположную сторону в отношении синусов этих углов.
- Линии, проведенные из вершин треугольника Лаунхардта к центрам масс каждого из больших треугольников, образуют параллелограмм.
Треугольник Лаунхардта имеет различные применения в геометрии и механике. В геометрии он используется, например, для нахождения площади или периметра треугольника. Также он применяется в механике для моделирования силы, действующей на объект в определенной точке.
Определение треугольника Лаунхарда
Этот треугольник определяется как треугольник, в котором сумма квадратов его высот равна сумме квадратов его сторон.
Пусть треугольник Лаунхарда имеет стороны a, b и c, а его высоты, опущенные из вершин на соответствующие стороны, обозначены как ha, hb и hc. Тогда может быть записана следующая формула:
a2 + b2 + c2 = ha2 + hb2 + hc2
Треугольник Лаунхарда имеет ряд интересных свойств и отличается от обычного треугольника. Этот тип треугольника имеет значение в геометрии и математической физике, а также находит свое применение в некоторых задачах конструирования и моделирования.
Что такое треугольник Лаунхарда?
Основное свойство треугольника Лаунхарда заключается в том, что он является треугольником с прямыми углами, а все его стороны являются целыми числами. Это делает его особенно интересным и полезным для исследования в контексте теории чисел и геометрии.
Одно из применений треугольника Лаунхарда связано с поиском так называемых «пифагоровых троек» — троек целых чисел (a, b, c), для которых выполняется теорема Пифагора: a^2 + b^2 = c^2. Треугольник Лаунхарда предоставляет особые значения для сторон треугольников, удовлетворяющих этому условию, что делает его особенно полезным инструментом при решении задач, связанных с теорией чисел и геометрии.
Треугольник Лаунхарда также находит применение в других областях, таких как математическое моделирование, компьютерная графика и криптография. Его уникальные свойства и возможности делают его одним из ключевых объектов изучения в математике и науке в целом.
| Стороны треугольника Лаунхарда | Прямые углы |
|---|---|
| 3 | 90° |
| 4 | 90° |
| 5 | 90° |
Структура и особенности треугольника Лаунхарда
Основной особенностью треугольника Лаунхарда является то, что он может быть построен на основе трех произвольных точек на плоскости, что отличает его от других типов треугольников, для которых есть определенные условия построения. Благодаря этому свойству, треугольник Лаунхарда находит широкое применение в математике и геометрии.
Треугольник Лаунхарда имеет три стороны и три угла, которые обозначаются как A, B и C. Каждый угол имеет свою меру, которая может быть измерена в градусах или радианах. Сумма мер трех углов всегда равна 180 градусов или Пи радианов.
Структура треугольника Лаунхарда определяется его сторонами и углами. Он может быть разносторонним, когда все его стороны имеют разные длины, равнобедренным, когда две стороны равны, или равносторонним, когда все три стороны равны. Кроме того, углы треугольника Лаунхарда могут быть остроугольными, прямоугольными или тупоугольными в зависимости от их меры.
Треугольник Лаунхарда является важным объектом исследования в математике и геометрии. Его свойства и особенности помогают углубить понимание треугольников в целом и применить этот знакомый геометрический объект в различных задачах и вычислениях. Понимание структуры и особенностей треугольника Лаунхарда поможет применять его свойства в практических и теоретических задачах.
Свойства треугольника Лаунхарда
- Треугольник Лаунхарда всегда является остроугольным треугольником. Это означает, что все его углы меньше 90 градусов.
- Сумма длин двух сторон треугольника Лаунхарда всегда больше длины третьей стороны.
- Одна из вершин треугольника Лаунхарда всегда находится посередине отрезка, соединяющего две другие вершины треугольника. Эта вершина называется точкой Лаунхарда или точкой пересечения биссектрис.
- При соединении вершин треугольника Лаунхарда соответствующими точками пересечения биссектрис получается новый треугольник, называемый треугольником Лаунхарда. В этом треугольнике точки пересечения биссектрис делят свои стороны в одинаковых отношениях.
Свойства треугольника Лаунхарда делают его интересным объектом в геометрии и находят применение в различных задачах и доказательствах. Они также помогают лучше понять структуру и связи внутри треугольника.
Основные свойства треугольника Лаунхарда
- У треугольника Лаунхарда все стороны равны между собой.
- Все углы треугольника Лаунхарда равны 60 градусов.
- Высоты треугольника Лаунхарда являются медианами и медиатрисами одновременно.
- Треугольник Лаунхарда является равносторонним треугольником.
- Окружность, описанная вокруг треугольника Лаунхарда, имеет радиус равный половине стороны треугольника.
- Треугольник Лаунхарда является самоподобным.
Из-за этих свойств треугольник Лаунхарда имеет множество применений в различных областях, включая геометрию, физику и математику.
Законы и теоремы, связанные с треугольником Лаунхарда
Закон синусов: в треугольнике Лаунхарда со сторонами a, b и c и соответствующими противолежащими углами A, B и C справедлива следующая формула:
(a / sinA) = (b / sinB) = (c / sinC)
Закон синусов позволяет вычислить длину неизвестной стороны или меру неизвестного угла треугольника Лаунхарда, если известны длины двух сторон и мера угла, не противолежащего этим сторонам.
Закон косинусов: в треугольнике Лаунхарда со сторонами a, b и c и углами A, B и C, справедлива следующая формула:
a^2 = b^2 + c^2 — 2bc * cosA
b^2 = a^2 + c^2 — 2ac * cosB
c^2 = a^2 + b^2 — 2ab * cosC
Закон косинусов позволяет вычислить длину неизвестной стороны треугольника Лаунхарда, если известны длины двух других сторон и мера угла, величина которого образована этими сторонами.
Применение треугольника Лаунхарда в экономике
В экономике треугольник Лаунхарда активно используется для определения оптимального баланса между безработицей и инфляцией, который называется «естественной безработицей». Идея заключается в том, что существует определенный уровень безработицы, который не может быть устранен полностью без вызова инфляции.
Диаграмма Лаунхарда позволяет экономистам и политикам принять решение о необходимых мерах для достижения устойчивого равновесия между безработицей и инфляцией. Она позволяет анализировать взаимосвязь между двумя показателями и предлагает различные стратегии для достижения желаемых результатов.
Применение треугольника Лаунхарда в экономике имеет широкий спектр возможностей. Он может быть использован для определения эффективности макроэкономической политики и оценки ее последствий. Также он может быть использован для исследования влияния экономических реформ, изменений в структуре рынка и других факторов на уровень безработицы и инфляции.
В целом, треугольник Лаунхарда является мощным инструментом для анализа и планирования экономической политики. Он позволяет ученым и политикам лучше понять и улучшить экономическую ситуацию в стране, что способствует развитию и процветанию национальной экономики.
Видео:
Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnline
Рекомендуем:
Влияние Европейского союза на мировое хозяйство — анализ и перспективы Комитет общественного спасения во Франции 18 века — создание и руководство — политическая борьба и роль Красного Террора в рамках Французской Революции Иван 2 Красный – история жизни, период правления и ключевые эпизоды Экономическое развитие торговли — ключевые факторы успеха и перспективы роста продаж Налоговая система РФ — главные задачи, проблемы и пути ее развития и совершенствования Организация антиинфляционной политики в России — принципы, инструменты и перспективы борьбы с высокими ценами Развитие рынка капитала в России — анализ современного состояния и будущие перспективы Основные признаки рыночной экономики — характеристики и основополагающие принципы, обеспечивающие высокую эффективность и конкурентоспособность Как правильно применять экономические системы и повышать эффективность бизнеса — полное руководство для успеха Развитие экономической науки в России — особенности, вызовы и перспективы на фоне глобальных экономических тенденций 