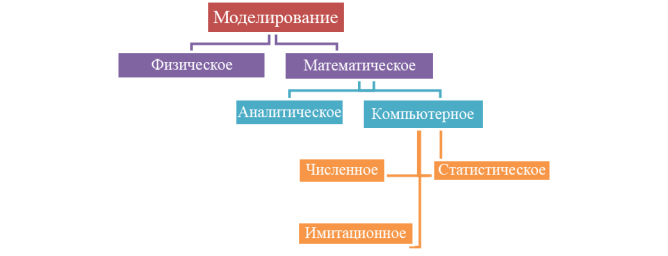
Математические методы моделирования в экономике — инструмент разработки оптимальных стратегий в условиях неопределенности и риска

Математическое моделирование — это процесс создания абстрактной модели реального объекта или системы с использованием математических методов. В экономике математическое моделирование является важным инструментом для анализа и прогнозирования поведения рынка, принятия решений и оптимизации производственных процессов. Оно позволяет исследовать различные экономические явления и процессы, а также предсказывать их будущее развитие.

Основные принципы математического моделирования в экономике включают построение формального математического описания объекта или системы, определение связей и зависимостей между его элементами, анализ полученной модели и прогнозирование результатов на основе различных сценариев и вариантов развития событий.

Применение математических методов моделирования в экономике широко распространено. Оно используется для решения различных задач — от определения оптимального размера производства и выбора наиболее эффективных стратегий до анализа взаимодействия различных экономических агентов и изучения влияния изменений в макроэкономической среде.

Математические модели могут быть представлены в виде уравнений, графов, систем дифференциальных уравнений и других математических конструкций. Их анализ позволяет исследовать различные варианты поведения объектов и систем в условиях изменяющихся параметров и факторов. Так, математические модели позволяют проводить прогнозы и определять наиболее эффективные стратегии развития экономических объектов.

Например, моделирование экономического рынка может позволить предсказать будущую цену товара или спрос на него при различных условиях. Или модель производственного процесса может помочь определить оптимальный объем производства и наилучшую схему управления ресурсами. Математическое моделирование также используется в финансовой аналитике, прогнозировании инфляции, изучении влияния налоговых изменений на экономические показатели и многих других областях экономики.

Математические методы моделирования в экономике

Математические методы моделирования играют важную роль в экономике, позволяя исследовать различные экономические явления и принимать рациональные решения.

Один из основных принципов математического моделирования в экономике — построение формальных моделей, которые описывают экономические процессы и связи между ними. Эти модели могут быть как аналитическими, основанными на математических уравнениях и системах, так и стохастическими, учитывающими случайные факторы.

Математические модели позволяют анализировать и прогнозировать эффекты изменений в экономической системе. Они могут помочь определить оптимальные стратегии и решения, прогнозировать спрос и предложение, оценить риски и выбрать наиболее выгодные варианты.

Одним из наиболее распространенных математических методов моделирования в экономике является линейное программирование. Оно позволяет оптимизировать распределение ресурсов и найти оптимальное решение задачи. Важным элементом линейного программирования является постановка целевой функции, которую нужно оптимизировать в рамках заданных ограничений.

Другим распространенным методом является статистическое моделирование. Оно используется для анализа данных и построения статистических моделей, которые могут прогнозировать будущие значения на основе имеющихся данных. Статистическое моделирование может быть применено для анализа экономических временных рядов, оценки рисков и вероятностных распределений.

Также существуют и другие математические методы моделирования в экономике, такие как динамическое программирование, теория игр, теория оптимального управления и др. Каждый метод имеет свои особенности и применяется в зависимости от поставленной задачи и доступных данных.

Основные принципы математического моделирования в экономике

Основные принципы математического моделирования в экономике включают следующие:

1. Упрощение и абстракция. При разработке экономической модели необходимо выделить самые существенные факторы, играющие роль в исследуемом процессе, и проигнорировать все остальные. Это позволяет создать упрощенную абстрактную модель, которая отражает основные закономерности поведения экономической системы.
2. Формализация. Экономическая модель должна быть представлена в формальной математической форме, которая позволяет проводить точные вычисления и давать количественные оценки. Формализация позволяет устанавливать четкие соотношения между переменными и параметрами модели.
3. Валидация и верификация. После разработки модели необходимо проверить ее на корректность и соответствие реальности. Валидация модели включает проверку соответствия полученных результатов наблюдаемым данным. Верификация модели включает тестирование программного кода и математических выкладок. Валидация и верификация позволяют убедиться в правильности и достоверности модели.

Математическое моделирование является неотъемлемой частью современной экономической науки. Оно позволяет исследовать сложные экономические процессы, строить прогнозы и оптимизировать решения. Основные принципы математического моделирования в экономике помогают научным исследователям и экономистам создавать адекватные и полезные модели, которые позволяют понять и объяснить поведение экономических систем.

Применение математических методов для описания экономических явлений

Математические методы играют важную роль в понимании и описании экономических процессов. Они позволяют строить модели, которые отражают структуру и динамику экономики, а также предсказывают состояние и поведение экономических систем.

В экономике часто применяются методы оптимизации, которые позволяют найти оптимальные решения с учетом ограничений и целей. Оптимизационные модели помогают определить наиболее эффективный способ использования ограниченных ресурсов, максимизировать прибыль или минимизировать затраты.

Другим важным инструментом математического анализа в экономике является теория игр. Теория игр изучает стратегии принятия решений в условиях конкуренции и взаимодействия различных участников. Она позволяет анализировать стратегические ситуации и прогнозировать поведение экономических агентов.

Таким образом, применение математических методов в экономике помогает объяснить сложные экономические явления, разработать эффективные стратегии и принять рациональные экономические решения.

Важность использования математических моделей в экономическом анализе

Использование математических моделей в экономическом анализе обладает несколькими преимуществами:

1.	Точность и объективность. Математические модели позволяют формализовать и структурировать экономическую информацию, что позволяет получить более точные и объективные результаты.
2.	Предсказательная способность. Математические модели позволяют прогнозировать будущие экономические события и тенденции, что помогает принимать рациональные решения на основе информации ожидаемого поведения экономики.
3.	Способность анализировать сложные системы. С помощью математических моделей можно исследовать взаимодействия между различными экономическими факторами и оценить их влияние на общий экономический процесс.
4.	Эффективность. Использование математических моделей позволяет проводить анализ экономических данных на больших объемах, автоматизировать процесс анализа и упрощает представление результатов.

Тем не менее, следует отметить, что математические модели не являются панацеей для всех проблем экономического анализа. Они не могут полностью учесть все факторы и особенности реального мира, поэтому необходимо применять их с осторожностью и анализировать полученные результаты в контексте экономической теории и практики.

Принципы построения математических моделей в экономике

В построении математических моделей в экономике существуют основные принципы, которые помогают научиться адекватно описывать и предсказывать экономические явления и процессы.

• Упрощение сложных явлений: В экономике часто встречаются сложные и многомерные явления. Однако, при построении математических моделей следует стремиться к их упрощению. Используя различные предположения и аппроксимации, можно создать более понятные и управляемые модели.
• Выбор релевантных переменных: При построении модели необходимо определить наиболее значимые переменные, которые влияют на изучаемый экономический процесс. Выбор релевантных переменных позволяет сосредоточиться на наиболее важных аспектах моделирования и уйти от излишней детализации.
• Формализация отношений: В математических моделях важно формализовать отношения между переменными, такие как причинно-следственные связи или зависимости. Это позволяет явно описать взаимодействия между различными компонентами экономической системы.
• Валидация модели: Одним из важных этапов в построении математических моделей является их валидация. Валидация предполагает сравнение результатов моделирования с реальными экономическими данными, оценку степени соответствия и адекватности модели рассматриваемой экономической системе.
• Прогнозирование и сценарный анализ: Одной из главных целей математического моделирования в экономике является возможность проведения прогнозов и сценарного анализа. Математические модели позволяют оценить влияние различных факторов на экономические показатели и установить оптимальные стратегии развития.

В итоге, математические модели в экономике помогают лучше понять и объяснить сложные экономические процессы, предсказать их развитие и принять более обоснованные решения в бизнесе и управлении экономикой.

Приложения математического моделирования в экономике

Математическое моделирование играет важную роль в экономике, позволяя исследовать различные аспекты экономической системы и принимать обоснованные решения. В этом разделе мы рассмотрим основные приложения математического моделирования в экономике.

1. Моделирование спроса и предложения.

   Математическое моделирование позволяет анализировать спрос и предложение на товары и услуги, определять оптимальные цены и объемы производства. Модели спроса и предложения основаны на экономической теории и статистических данных и позволяют прогнозировать изменения рыночных условий и предсказывать результаты различных экономических политик.
2. Оптимизация инвестиционных портфелей.

   Математическое моделирование используется для создания оптимальных портфелей инвестиций. Модели учитывают риск и доходность различных инвестиционных активов, а также предлагают стратегии диверсификации и управления риском. Оптимизация портфелей позволяет инвесторам принимать обоснованные решения и минимизировать потенциальные потери.

3. Моделирование рынка труда.

   Математические модели рынка труда позволяют анализировать взаимодействие между спросом на рабочую силу и ее предложением. Модели учета безработицы, заработной платы, поиска работы и других факторов позволяют оценивать эффективность различных политик занятости и прогнозировать изменения на рынке труда.

4. Моделирование экономического роста.

   Математическое моделирование экономического роста позволяет изучать факторы, влияющие на долгосрочный экономический рост. Модели учитывают такие переменные, как инвестиции, технологический прогресс и капиталовложения, и позволяют анализировать различные политики развития и их влияние на экономический рост.

Это лишь некоторые из приложений математического моделирования в экономике. Данный подход исследования экономических вопросов позволяет экономистам и руководителям принимать обоснованные решения на основе количественной оценки и прогнозирования различных экономических сценариев.

Моделирование рыночных процессов и прогнозирование тенденций

Одним из наиболее распространенных методов моделирования рыночных процессов является использование статистических моделей, таких как регрессионный анализ. Этот метод позволяет изучить зависимость между различными факторами и их влияние на рыночную динамику. На основе этих данных можно построить модель, которая будет описывать и прогнозировать рыночные тенденции.

Кроме статистических моделей, в экономике также широко используются симуляционные модели. Они позволяют моделировать сложные звенья и взаимосвязи между участниками рынка, учесть различные факторы, такие как спрос и предложение, конкуренцию, изменение цен и тому подобное. Симуляционные модели предоставляют возможность провести эксперименты и оценить возможные результаты различных стратегий и решений.

Прогнозирование тенденций рыночных процессов осуществляется с использованием различных методов, таких как временные ряды и эконометрические модели. Они позволяют анализировать прошлые данные и на их основе делать прогнозы на будущее. Прогнозирование позволяет предугадать изменения спроса и предложения на рынке, ценообразование, конкуренцию и другие факторы, которые могут повлиять на успех предприятия.

Моделирование рыночных процессов и прогнозирование тенденций играют важную роль в различных областях экономики, таких как финансы, маркетинг, стратегическое планирование и решение проблем. Они помогают прогнозировать возможные риски, лучше понимать рынок и его динамику, а также принимать рациональные и взвешенные решения.

Видео:

КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕ